AW 5
Thema: Zahlen und Diagramme richtig lesen und verstehen

zurück zur Übersicht: Das kann man lernen …

Was ist ein Diagramm?

Ein Diagramm ist die grafische Darstellung von gezählten oder gemessenen Werten.
Es besteht immer eine zahlenmäßige Abhängigkeit zwischen zwei oder mehr Größen, z.B. der Temperatur und der Zeit.

Warum wird ein Diagramm erstellt?

Ein Wissenschaftler hat z.B. über den Tag hinweg die Temperaturen in einem Waldstück gemessen. Nun will er dir den Temperaturverlauf beschreiben. In Worten würde dieses sehr lange dauern und schwer verständlich sein. Mithilfe eines erstellten Diagramms kann jeder schnell sehen und verstehen, wie hoch die Temperaturen im Wald zu einem bestimmten Zeitpunkt des Tages waren.

Wie wird ein Diagramm erstellt?

Der Wissenschaftler trägt die gemessenen Werte aus einer Wertetabelle in ein Koordinatensystem ein. Ein Koordinatensystem hat eine y-Achse und eine x-Achse.
Beide Achsen werden mit einer eigenen Maßeinheit versehen. Im Beispiel beschreibt der Wissenschaftler die Höhe der Temperatur durch eine Skala an der y-Achse (abhängige Variable, d.h. eine veränderbare Größe) und die Zeit durch eine Skala an der x-Achse (unabhängige Variable, d.h. eine festgelegte Größe).
Danach wird er die zu den verschiedenen Zeiten gemessenen Temperaturen – in Form von Punkten oder kleinen Symbolen – aus der Wertetabelle in dieses Koordinatensystem eintragen. Die eingetragenen Messwerte müssen nur noch miteinander verbunden werden und fertig ist das Kurvendiagramm.
Streng genommen dürfen wenige Einzelwerte nicht miteinander zu einer Kurve verbunden werden, da damit Zwischenwerte vorgetäuscht werden. Dennoch werden oft wenige Messwerte zu einer Linie miteinander verbunden. In diesem Fall sollte ein Hinweis auf diese Vorgehensweise erfolgen.
Es ist auch zu überlegen, ob die Werte – vor allem wenige Werte – besser als Balken-, Säulendiagramm oder Tortenabschnitte darzustellen sind.

Der folgende Link führt zu Erklärungen der in Microsoft-Office enthaltenen Diagrammtypen. Vergleichbare Diagrammtypen findet man auch in anderen Programmen (OpenOffice, Neo Office).

http://www.openoffice.org/de/doc/oooauthors/calc/04-diagramme-und-graphen-erstellen.pdf (Zugriff: 2015-06-14)
http://office.microsoft.com/de-de/excel-help/verfugbare-diagrammtypen-HA001233737.aspx (Zugriff: 2015-06-14)

Im Folgenden lernst du, wie ein Diagramm zu beschreiben und auszuwerten ist.

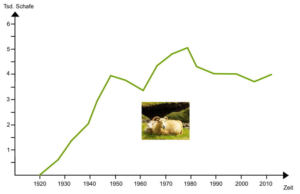
Schaue dir das Diagramm auf der folgenden Seite zunächst genau an.
Gehe erst dann zu Punkt B!
Beschreibe das Diagramm unter folgenden Gesichtspunkten:

Was ist dargestellt? (Thema des Diagramms)
Wie sind die Werte grafisch dargestellt? (Kurve, Säulen-, Kreisdiagramm, etc.)
Was wird miteinander verglichen bzw. gegenübergestellt?
Benennung der Achsen: Was ist auf der y-Achse (abhängige Variable) und was auf
der x-Achse (unabhängige Variable) dargestellt?
Welche Einheiten stehen an den Achsen?
Wie sehen die Veränderungen im Verlaufe des Diagramms entlang der x-Achse aus? (Anfangspunkt, Angaben zur Steigung [ansteigen, fallen, sinken, steigen, leicht, stark, allmählich, gleichmäßig, abrupt], Maximal- und Minimalwerte, Ausnahmen, Endpunkt)
Aber: Dabei geht es nicht um eine rein mathematische Beschreibung von Werten, sondern es ist immer ein Bezug zu den dargestellten Größen herzustellen!
Bei der Darstellung mehrerer Kurven: Welche Gemeinsamkeiten und Unterschiede gibt es in den Kurvenverläufen?

Auswertung / Erläuterung des Diagramms

Welche Aussage(n) lässt das Diagramm zu?
Welche Schlussfolgerung(en) lässt das Diagramm zu?
Lassen sich eine Regel oder Gesetzmäßigkeit (zumindest als Hypothese) ableiten?
Gibt es dir bekannte biologische Grundlagen (Regeln, Gesetzmäßigkeiten), die in diesem Zusammenhang eine Rolle spielen (könnten)?
Welche weiteren Informationen benötigst du, um die Regel, Gesetzmäßigkeit oder Hypothese zu bestätigen oder zu verwerfen?
Gibt es unerklärliche Sachverhalte und worauf könnten diese zurückzuführen sein (z.B. Versuchsdurchführungsfehler, Messungenauigkeiten etc.)?

Übe anhand der beiden folgenden Abbildungen das Lesen und Verstehen von Diagrammen.

Abb. AW 5-1 Entwicklung einer Islandschafherde (-population) auf einer Insel

Abb. AW 5-2 Fotosynthese und Atmung bei einer Pflanze im Verlaufe eines Tages

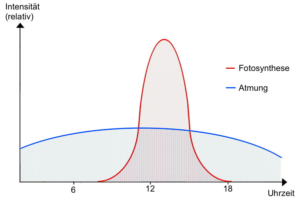
Hinweis: Das Wort „relativ“ meint, dass die Kurven nicht die exakten Messwerte anzeigen, sondern nur das Verhältnis zwischen beiden Prozessen widerspiegeln.

Die folgenden drei Diagramme enthalten jeweils Werte zur Anzahl von vorgenommenen Facebook-Einträgen im Verlauf von 10 Jahren.
Klicke den Button an, betrachte kurz jedes Diagramm und entscheide spontan, in welchem Fall die Anzahl vorgenommener Einträge am stärksten in den letzten 10 Jahren gestiegen ist( A, B oder C).

Darstellung der drei Diagramme A, B und C:

Abb. AW 5-3 Unterschiedliche Darstellung von Zahlen in Diagrammen

Lösung Aufg.2:

Alle drei Fälle sind identisch!
Es handelt sich hierbei um ein Beispiel, wie man durch Manipulation – in diesen Fällen Änderung der Skalierung – Aussagen von Zahlen verfälschen kann.

Fast täglich begegnen uns Darstellung von Zahlen in den Medien. Prüfe immer genau, wie etwas dargestellt wird! Du wirst leider bemerken, dass derartige Verfälschungen sehr häufig sind, vor allem dann, wenn jemand damit eine bestimmte Meinung erzeugen möchte.
Wer sich damit etwas genauer beschäftigen möchte, findet unter den folgenden Links weitere Beispiele und Erläuterung zur Manipulation mit Zahlen.

https://www.youtube.com/watch?v=SNFciqw8tDs (Zugriff: 2021-05-05)
https://www.youtube.com/watch?v=PC1Dw1lfLtI (Zugriff: 2021-05-05)
https://www.youtube.com/watch?v=UVWJYAgX5Es (Zugriff: 2021-05-05)
https://www.youtube.com/watch?v=31N-qv6Twvk (Zugriff: 2016-06-15)
https://www.spektrum.de/video/daten-wie-man-mit-statistiken-luegen-kann/1733666 (Zugriff: 2023-08-03)

https://docplayer.org/22139682-Luegen-mit-statistik-johannes-kepler-gymnasium-das-plenum-deckt-auf-luegen-mit-statistik-plenum-luegen-mit-statistik-mathematik-jahrgangsstufe-11.html (Zugriff: 2019-08-13)
https://de.statista.com/statistik/lexikon/definition/8/luegen_mit_statistiken/ (Zugriff: 2020-08-13)
http://www.wdr.de/tv/applications/fernsehen/wissen/quarks/pdf/Q_Zahlen.pdf (Zugriff: 2016-06-15)
https://www.rwi-essen.de/unstatistik (Zugriff: 2019-03-09)In Zusammenhang mit Ernährung siehe auch:
„Fleisch – drei viel diskutierte Fragen“

1. Stimmt das?
  „Der Storch bringt die Babys!“
  Das wolltest du nie glauben, doch es gibt einen eindeutigen statistischen Nachweis dafür, dass die „Geburtenrate“ und die „Anzahl der Störche“ stark miteinander korrelieren. „Korrelieren“ bedeutet, dass zwei Werte statistisch-mathematisch nachweisbar voneinander abhängig sind.
  Finde diesen Beweis im Internet, in dem du die beiden Suchbegriffe „Geburtenrate“ und „Störche“ gemeinsam verwendest. Du wirst dort auch Kurvendiagramme finden, die das belegen. (Leider aus Gründen des Copyrights hier nicht abbildbar!)
  
  Abb. AW 5-4
  Der Storch bringt die Babys!

Wo liegt der grundsätzliche Fehler dieses angeblichen Beweises?
Die Beantwortung der Frage findest du z.B. unter folgenden Links:
https://home.uni-leipzig.de/schreibportal/korrelation-als-kausalitaet/ (Zugriff: 2020-01-08)
https://www.crashkurs-statistik.de/korrelation-und-kausalitaet/?cookie-state-change=1580829380056 (Zugriff: 2020-01-30)
https://home.uni-leipzig.de/schreibportal/korrelation-als-kausalitaet/ (Zugriff: 2020-01-30)
http://beza1e1.tuxen.de/articles/korrelation_vs_kausalitaet.html (Zugriff: 2020-01-30)
http://methoden-psychologie.de/korrelation_kausalitaet.html (Zugriff: 2020-01-30)

Mit Zahlen kann man irreführen, täuschen und manipulieren. Aber haben Zahlen auch einen ethischen Wert, d.h. dass Zahlen auch „das sittliche Verhalten des Menschen“ betreffen können? Dazu folgendes Zitat eines Teilnehmers an der Anti-Corona-Demonstration vom 30.08.20 in Berlin:
„Das Übertriebene an den Maßnahmen gegen Covid 19 zeigt u.a. die Tatsache, dass lediglich 0,011 % der Weltbevölkerung daran gestorben ist.“
Diskutiere diese Aussage.

Daten zu 5.:

Ungefähr 7.755.000.000 Menschen bevölkern 2020 die Welt. Bis zum 01.09.2020 starben 848.000 Menschen in Zusammenhang mit Covid 19.

Weitere Beispiele und Grundlagen findet man hier:

https://www.uni-regensburg.de/assets/mathematik/didaktik-mathematik/lehrerfortbildungen/workshop_sol__gtmanmitstatistik_bruckmaier_schmei__er_p.pdf (U.-Konzept für Lehrkräfte /Zugriff: 2023-08-07)
https://www.rwi-essen.de/presse/wissenschaftskommunikation/unstatistik (Zugriff: 2023-08-07)

Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung – Weitergabe unter gleichen Bedingungen 4.0 International Lizenz.